Some time ago, I posted a banal case to show the limits of K-mean clustering. A follower gave us a grid of different clustering techniques (calling internal routines of Mathematica) to solve the case discussed.
As you know, I like to write by myself the algorithms and I like to show alternative paths, so I’ve decided to explain a powerful clustering algorithm based on the SVM.
Some time ago, I posted a banal case to show the limits of K-mean clustering. A follower gave us a grid of different clustering techniques (calling internal routines of Mathematica) to solve the case discussed.
As you know, I like to write by myself the algorithms and I like to show alternative paths, so I’ve decided to explain a powerful clustering algorithm based on the SVM.
To understand the theory behind SVC (support vector clustering) I strongly recommend you have a look at: http://jmlr.csail.mit.edu/papers/volume2/horn01a/rev1/horn01ar1.pdf . In this paper you will find all of the technical details explained with extremely clarity.
As usual I leave the theory to the books and I jump into the pragmatism of the real world.
Consider the problem of a set of points having an ellipsoid distribution: we have seen in the past that K-means doesn’t work in this scenario, and even trying different tweaks changing the position of the centroids and its number of centroids, the final result is always unacceptable.
SVC is a clustering algorithm that takes as input just two parameters (C and q) both of them real numbers. C is to manage the outliers and q is to manage the number of clusters. Be aware that q is not directly related with the number of clusters!! Tuning q you can manage the “cluster granularity” but you cannot decide a priori the number of clusters returned by the algo.
How to implement SVC.
There are many implementations of SVC, but I would like to show different tools (I love broadening the horizons…), so the ingredients of the daily recipe are: AMPL & SNOPT.
Both of them are commercial tools but to play with small set of points (no more than 300) you can use for free the student license!
AMPL is a comprehensive and powerful algebraic modeling language for linear and nonlinear optimization problems, in discrete or continuous variables and SNOPT is a software package for solving large-scale optimization problems (linear and nonlinear programs).
AMPL allows the user to write the convex problem associated to SVC’s problem in easy way:
 |
| The AMPL file for SVC |
And SNOPT is one of the many solvers ables to work with AMPL.
Let’s show the application of SVC in our ellipsoid data set
 |
| 300 pt having ellipsoid distribution. The first contour of SVC has been depicted in black. |
3D problem
Just to show the same algorithm working in 3D on the same problem:
 |
| 3D points having ellipsoid distribution. |
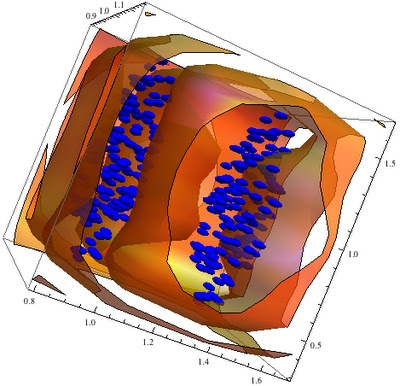 |
| SVC applied on the former data set |





