…Usually such behavior is not proficient to obtain good results, but this time I think that the change of prospective has been positive!
…Usually such behavior is not proficient to obtain good results, but this time I think that the change of prospective has been positive!
Chebyshev Theorem
In many real scenarios (under certain conditions) the Chebyshev Theorem provides a powerful algorithm to detect outliers.
The method is really easy to implement and it is based on the distance of Zeta-score values from k standard deviation.
…Surfing on internet you can find several explanations and theoretical explanation of this pillar of the Descriptive Statistic, so I don’t want increase the Universe Entropy explaining once again something already available and better explained everywhere 🙂
Approach based on Mutual Information
Before I explain my approach I have to say that I have not had time to check in literature if this method has been already implemented (please drop a comment if someone finds out a reference! … I don’t want take improperly credits).
The aim of the method is to remove iteratively the sorted Z-Scores till the mutual information between the Z-Scores and the candidates outlier I(Z|outlier) increases.
At each step the candidate outlier is the Z-score having the highest absolute value.
Basically, respect the Chebyschev method, there is no pre-fixed threshold.
Experiments
I compared the two methods through canonical distribution, and at a glance it seems that results are quite good.
 |
| Test on Normal Distribution |
As you can see in the above experiment the Mutual information criteria seems more performant in the outlier detection.
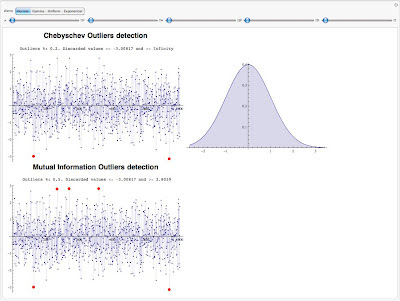 |
| Test on Normal Distribution having higher variance |
The following experiments have been done with Gamma Distribution and Negative Exponential
 |
| Results on Gamma seem comparable. |
 |
| Experiment done using Negative Exponential distribution |
…In the next days I’m going to test the procedure on data having multimodal distribution.
Stay Tuned
Cristian






